Portal:Mathematics

• 
  Abacus, a ancient hand-operated calculating.
• 
  Portrait of Emmy Noether, around 1900.
• 
  Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

• 

  

  The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

  
  
  In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
  $$\sum _{n=1}^{m}n(-1)^{n-1}.$$
  
  The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
  $$1-2+3-4+\cdots ={\frac {1}{4}}.$$ (Full article...)
• 
  
  

  

  Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

  
  An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.
  
  While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
• 
  
  

  

  A stamp of Zhang Heng issued by China Post in 1955

  
  Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
  
  Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
• 
  
  

  

  Elementary algebra studies which values solve equations formed using arithmetical operations.

  
  Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
  
  Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
• 
  The number π (/paɪ/ ^ⓘ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.
  
  The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as ${\tfrac {22}{7}}$ are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
• 
  General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
  present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
  
  Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
• 

  

  
  Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.
  
  In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
• 
  
  

  

  Rejewski, c. 1932

  
  Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ^ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
  
  Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
• 
  
  

  

  Bust of Shen at the Beijing Ancient Observatory

  
  Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).
  
  In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
• 

  

  
  Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
  
  Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
• 
  
  

  

  Cantor, c. 1910

  
  Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
  
  Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
• 

  

  The manipulations of the Rubik's Cube form the Rubik's Cube group.

  
  In mathematics, a group is a set with an operation that associates every pair of elements of the set to an element of the set (as does every binary operation) and satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.
  
  Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠$1$⁠ (these properties characterize the integers in a unique way). (Full article...)
• 

  

  Logic studies valid forms of inference like modus ponens.

  
  
  Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
  
  Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)

Good articles

• 
  Sunday Osarumwense Iyahen (3 October 1937 – 28 January 2018) was a Nigerian mathematician and politician, recognised for his contributions to the field of topological vector spaces and his service as a senator representing Bendel Central Senatorial District. Born in Benin City, Edo State, Nigeria, Iyahen was the eldest of at least seventeen children and embarked on an academic journey that led him to earn a first-class honours degree in mathematics from the University of Ibadan and later a Ph.D. and D.Sc. from the University of Keele.
  
  Iyahen's academic career was marked by his tenure as a professor of mathematics at several universities in Nigeria and abroad. He served as the Head of the Department of Mathematics and Dean of the Faculty of Science at the University of Ibadan before joining the Institute of Technology, Benin (now known as the University of Benin), where he became the founding dean of the Faculty of Physical Sciences. His scholarly work includes over 100 published papers and contributions as editor-in-chief for mathematical journals. He was honoured with fellowships from the Nigerian Academy of Science and the Mathematical Association of Nigeria. As a politician, he was elected as a senator, where he contributed to national policy and development. (Full article...)
• 
  
  

  

  Wigner in 1963

  
  Eugene Paul Wigner (Hungarian: Wigner Jenő Pál, pronounced [ˈviɡnɛr ˈjɛnøː ˈpaːl]; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles".
  
  A graduate of the Technical Hochschule Berlin (now Technische Universität Berlin), Wigner worked as an assistant to Karl Weissenberg and Richard Becker at the Kaiser Wilhelm Institute in Berlin, and David Hilbert at the University of Göttingen. Wigner and Hermann Weyl were responsible for introducing group theory into physics, particularly the theory of symmetry in physics. Along the way he performed ground-breaking work in pure mathematics, in which he authored a number of mathematical theorems. In particular, Wigner's theorem is a cornerstone in the mathematical formulation of quantum mechanics. He is also known for his research into the structure of the atomic nucleus. In 1930, Princeton University recruited Wigner, along with John von Neumann, and he moved to the United States, where he obtained citizenship in 1937. (Full article...)
• 

  

  
  In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.
  
  The theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, sometimes called the Pythagorean equation:
  :$a^{2}+b^{2}=c^{2}.$
  The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. (Full article...)
• 

  

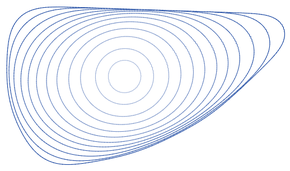
  Convergence of a convex curve to a circle under the curve-shortening flow. Inner curves (lighter color) are flowed versions of the outer curves. Time steps between curves are not uniform.

  
  In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.
  
  As the points of any smooth simple closed curve move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its total absolute curvature decreases monotonically, until it becomes convex. Once convex, the isoperimetric ratio of the curve decreases as the curve converges to a circular shape, before collapsing to a singularity. If two disjoint simple smooth closed curves evolve, they remain disjoint until one of them collapses to a point. (Full article...)
• 

  

  A Möbius strip made with paper and adhesive tape

  
  In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.
  
  As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a single boundary curve. (Full article...)
• 

  

  The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle. All points on a side are equidistant from the opposite vertex.

  
  A Reuleaux triangle [ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"
  
  They are named after Franz Reuleaux, a 19th-century German engineer who pioneered the study of machines for translating one type of motion into another, and who used Reuleaux triangles in his designs. However, these shapes were known before his time, for instance by the designers of Gothic church windows, by Leonardo da Vinci, who used it for a map projection, and by Leonhard Euler in his study of constant-width shapes. Other applications of the Reuleaux triangle include giving the shape to guitar picks, fire hydrant nuts, pencils, and drill bits for drilling filleted square holes, as well as in graphic design in the shapes of some signs and corporate logos. (Full article...)
• 

  

  
  In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. Because it has no interior diagonals, it cannot be triangulated into tetrahedra without adding new vertices. It has the fewest vertices of any polyhedron that cannot be triangulated. It is named after the German mathematician Erich Schönhardt, who described it in 1928, although the artist Karlis Johansons had exhibited a related structure in 1921.
  
  One construction for the Schönhardt polyhedron starts with a triangular prism and twists the two equilateral triangle faces of the prism relative to each other, breaking each square face into two triangles separated by a non-convex edge. Some twist angles produce a jumping polyhedron whose two solid forms share the same face shapes. A 30° twist instead produces a shaky polyhedron, rigid but not infinitesimally rigid, whose edges form a tensegrity prism. (Full article...)
• 
  In the mathematical fields of graph theory and finite model theory, the logic of graphs deals with formal specifications of graph properties using sentences of mathematical logic. There are several variations in the types of logical operation that can be used in these sentences. The first-order logic of graphs concerns sentences in which the variables and predicates concern individual vertices and edges of a graph, while monadic second-order graph logic allows quantification over sets of vertices or edges. Logics based on least fixed point operators allow more general predicates over tuples of vertices, but these predicates can only be constructed through fixed-point operators, restricting their power.
  
  A sentence $S$ may be true for some graphs, and false for others; a graph $G$ is said to model $S$, written $G\models S$, if $S$ is true of the vertices and adjacency relation of $G$. The algorithmic problem of model checking concerns testing whether a given graph models a given sentence. The algorithmic problem of satisfiability concerns testing whether there exists a graph that models a given sentence.
  Although both model checking and satisfiability are hard in general, several major algorithmic meta-theorems show that properties expressed in this way can be tested efficiently for important classes of graphs. (Full article...)
• 

  

  Squaring the circle: the areas of this square and this circle are both equal to π. In 1882, it was proven that this figure cannot be constructed in a finite number of steps with an idealized compass and straightedge.

  
  Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square with the area of a given circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a square.
  
  In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi ($\pi$) is a transcendental number.
  That is, $\pi$ is not the root of any polynomial with rational coefficients. It had been known for decades that the construction would be impossible if $\pi$ were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been found. (Full article...)
• 

  

  Composite numbers can be arranged into rectangles but prime numbers cannot.

  
  
  A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
  
  The property of being prime is called primality. A simple but slow method of checking the primality of a given number ⁠$n$⁠, called trial division, tests whether ⁠$n$⁠ is a multiple of any integer between 2 and ⁠${\sqrt {n}}$⁠. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produces the correct answer in polynomial time but is too slow to be practical. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of October 2024 the largest known prime number is a Mersenne prime with 41,024,320 decimal digits. (Full article...)
• 

  

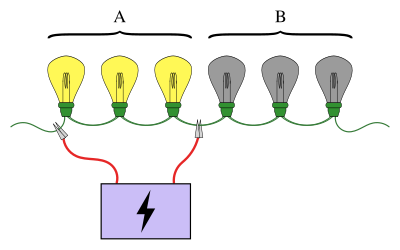
  An illustration of the lightbulb problem, where one is searching for a broken bulb among six lightbulbs. Here, the first three are connected to a power supply, and they light up (A). This indicates that the broken bulb must be one of the last three (B). If instead the bulbs did not light up, one could be sure that the broken bulb was among the first three. Continuing this procedure can locate the broken bulb in no more than three tests, compared to a maximum of six tests if the bulbs are checked individually.

  
  
  In statistics and combinatorial mathematics, group testing is any procedure that breaks up the task of identifying certain objects into tests on groups of items, rather than on individual ones. First studied by Robert Dorfman in 1943, group testing is a relatively new field of applied mathematics that can be applied to a wide range of practical applications and is an active area of research today.
  
  A familiar example of group testing involves a string of light bulbs connected in series, where exactly one of the bulbs is known to be broken. The objective is to find the broken bulb using the smallest number of tests (where a test is when some of the bulbs are connected to a power supply). A simple approach is to test each bulb individually. However, when there are a large number of bulbs it would be much more efficient to pool the bulbs into groups. For example, by connecting the first half of the bulbs at once, it can be determined which half the broken bulb is in, ruling out half of the bulbs in just one test. (Full article...)
• 
  Vedic Mathematics is a book written by Indian Shankaracharya Bharati Krishna Tirtha and first published in 1965. It contains a list of mathematical techniques which were falsely claimed to contain advanced mathematical knowledge. The book was posthumously published under its deceptive title by editor V. S. Agrawala, who noted in the foreword that the claim of Vedic origin, made by the original author and implied by the title, was unsupported.
  
  Neither Krishna Tirtha nor Agrawala were able to produce sources, and scholars unanimously note it to be a compendium of methods for increasing the speed of elementary mathematical calculations sharing no overlap with historical mathematical developments during the Vedic period. Nonetheless, there has been a proliferation of publications in this area and multiple attempts to integrate the subject into mainstream education at the state level by right-wing Hindu nationalist governments. (Full article...)

Did you know

• ... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
• ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
• ... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
• ... that two members of the French parliament were killed when a delayed-action German bomb exploded in the town hall at Bapaume on 25 March 1917?
• ... that owner Matthew Benham influenced both Brentford FC in the UK and FC Midtjylland in Denmark to use mathematical modelling to recruit undervalued football players?
• ... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
• ... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
• ... that Catechumen, a Christian first-person shooter, was funded only in the aftermath of the Columbine High School massacre?

Did you know...

• ...that there are different sizes of infinite sets in set theory? More precisely, not all infinite cardinal numbers are equal?
• ...that every natural number can be written as the sum of four squares?
• ...that the largest known prime number is nearly 41 million digits long?
• ...that the set of rational numbers is equal in size to the set of integers; that is, they can be put in one-to-one correspondence?
• ...that there are precisely six convex regular polytopes in four dimensions? These are analogs of the five Platonic solids known to the ancient Greeks.
• ...that it is unknown whether π and e are algebraically independent?
• ...that a nonconvex polygon with three convex vertices is called a pseudotriangle?

Featured pictures

• 
  Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
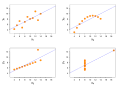
  Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals